跳跃表
# 引言
- 跳表 (Skip List) 是由 William Pugh 发明的一种查找数据结构,支持对数据的快速查找,插入和删除。
- 跳表的期望空间复杂度为$O(n)$,跳表的查询,插入和删除操作的期望时间复杂度都为$O(logn)$。
# 基本思想
顾名思义,跳表是一种类似于链表的数据结构。更加准确地说,跳表是对有序链表的改进。
为方便讨论,后续所有有序链表默认为 升序 排序。
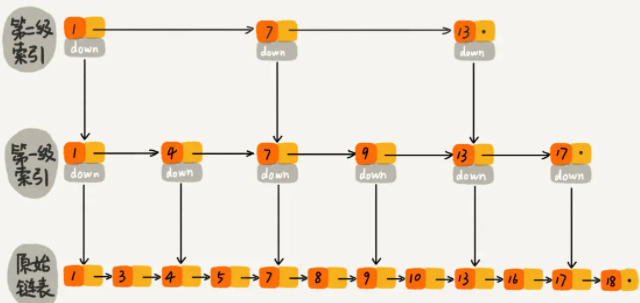
一个有序链表的查找操作,就是从头部开始逐个比较,直到当前节点的值大于或者等于目标节点的值。很明显,这个操作的复杂度是$O(n)$。 跳表在有序链表的基础上,引入了 分层 的概念。首先,跳表的每一层都是一个有序链表,特别地,最底层是初始的有序链表。每个位于第i层的节点有$p$的概率出现在第i+1层,$p$为常数。
记在 n 个节点的跳表中,期望包含$\frac{1}{p}$个元素的层为第$L(n)$层,易得$L(n) = log_{\frac{1}{p}}n$。
在跳表中查找,就是从第$L(n)$层开始,水平地逐个比较直至当前节点的下一个节点大于等于目标节点,然后移动至下一层。重复这个过程直至到达第一层且无法继续进行操作。此时,若下一个节点是目标节点,则成功查找;反之,则元素不存在。这样一来,查找的过程中会跳过一些没有必要的比较,所以相比于有序链表的查询,跳表的查询更快。可以证明,跳表查询的平均复杂度为$O(logn)$。
# 复杂度证明
# 空间复杂度

# 时间复杂度

# 具体实现
# 获取节点的最大层数
模拟以p的概率往上加一层,最后和上限值取最小。p的意义就是上一层的节点个数是下一层的1/p的概率。每一层都以这种规则来设置上一层的节点个数。
int randomLevel() {
int lv = 1;
// MAXL = 32, S = 0xFFFF, PS = S * P, P = 1 / 4
while ((rand() & S) < PS) ++lv;
return min(MAXL, lv);
}
# 查询
查询跳表中是否存在键值为 key 的节点。具体实现时,可以设置两个哨兵节点以减少边界条件的讨论。
V& find(const K& key) {
SkipListNode<K, V>* p = head;
// 找到该层最后一个键值小于 key 的节点,然后走向下一层
for (int i = level; i >= 0; --i) {
while (p->forward[i]->key < key) {
p = p->forward[i];
}
}
// 现在是小于,所以还需要再往后走一步
p = p->forward[0];
// 成功找到节点
if (p->key == key) return p->value;
// 节点不存在,返回 INVALID
return tail->value;
}
# 插入
插入节点 (key, value)。插入节点的过程就是先执行一遍查询的过程,中途记录新节点是要插入哪一些节点的后面,最后再执行插入。每一层最后一个键值小于 key 的节点,就是需要进行修改的节点。
void insert(const K &key, const V &value) {
// 用于记录需要修改的节点
SkipListNode<K, V> *update[MAXL + 1];
SkipListNode<K, V> *p = head;
for (int i = level; i >= 0; --i) {
while (p->forward[i]->key < key) {
p = p->forward[i];
}
// 第 i 层需要修改的节点为 p
update[i] = p;
}
p = p->forward[0];
// 若已存在则修改
if (p->key == key) {
p->value = value;
return;
}
// 获取新节点的最大层数
int lv = randomLevel();
if (lv > level) {
lv = ++level;
update[lv] = head;
}
// 新建节点
SkipListNode<K, V> *newNode = new SkipListNode<K, V>(key, value, lv);
// 在第 0~lv 层插入新节点
for (int i = lv; i >= 0; --i) {
p = update[i];
newNode->forward[i] = p->forward[i];
p->forward[i] = newNode;
}
++length;
}
# 删除
删除键值为 key 的节点。删除节点的过程就是先执行一遍查询的过程,中途记录要删的节点是在哪一些节点的后面,最后再执行删除。每一层最后一个键值小于 key 的节点,就是需要进行修改的节点。
bool erase(const K &key) {
// 用于记录需要修改的节点
SkipListNode<K, V> *update[MAXL + 1];
SkipListNode<K, V> *p = head;
for (int i = level; i >= 0; --i) {
while (p->forward[i]->key < key) {
p = p->forward[i];
}
// 第 i 层需要修改的节点为 p
update[i] = p;
}
p = p->forward[0];
// 节点不存在
if (p->key != key) return false;
// 从最底层开始删除
for (int i = 0; i <= level; ++i) {
// 如果这层没有 p 删除就完成了
if (update[i]->forward[i] != p) {
break;
}
// 断开 p 的连接
update[i]->forward[i] = p->forward[i];
}
// 回收空间
delete p;
// 删除节点可能导致最大层数减少
while (level > 0 && head->forward[level] == tail) --level;
// 跳表长度
--length;
return true;
}
# 完整代码
下列代码是用跳表实现的 map。未经正经测试,仅供参考。
#include <bits/stdc++.h>
using namespace std;
template <typename K, typename V>
struct SkipListNode {
int level;
K key;
V value;
SkipListNode **forward;
SkipListNode() {}
SkipListNode(K k, V v, int l, SkipListNode *nxt = NULL) {
key = k;
value = v;
level = l;
forward = new SkipListNode *[l + 1];
for (int i = 0; i <= l; ++i) forward[i] = nxt;
}
~SkipListNode() {
if (forward != NULL) delete[] forward;
}
};
template <typename K, typename V>
struct SkipList {
static const int MAXL = 32;
static const int P = 4;
static const int S = 0xFFFF;
static const int PS = S / P;
static const int INVALID = INT_MAX;
SkipListNode<K, V> *head, *tail;
int length;
int level;
SkipList() {
srand(time(0));
level = length = 0;
tail = new SkipListNode<K, V>(INVALID, 0, 0);
head = new SkipListNode<K, V>(INVALID, 0, MAXL, tail);
}
~SkipList() {
delete head;
delete tail;
}
int randomLevel() {
int lv = 1;
while ((rand() & S) < PS) ++lv;
return min(MAXL, lv);
}
void insert(const K &key, const V &value) {
SkipListNode<K, V> *update[MAXL + 1];
SkipListNode<K, V> *p = head;
for (int i = level; i >= 0; --i) {
while (p->forward[i]->key < key) {
p = p->forward[i];
}
update[i] = p;
}
p = p->forward[0];
if (p->key == key) {
p->value = value;
return;
}
int lv = randomLevel();
if (lv > level) {
lv = ++level;
update[lv] = head;
}
SkipListNode<K, V> *newNode = new SkipListNode<K, V>(key, value, lv);
for (int i = lv; i >= 0; --i) {
p = update[i];
newNode->forward[i] = p->forward[i];
p->forward[i] = newNode;
}
++length;
}
bool erase(const K &key) {
SkipListNode<K, V> *update[MAXL + 1];
SkipListNode<K, V> *p = head;
for (int i = level; i >= 0; --i) {
while (p->forward[i]->key < key) {
p = p->forward[i];
}
update[i] = p;
}
p = p->forward[0];
if (p->key != key) return false;
for (int i = 0; i <= level; ++i) {
if (update[i]->forward[i] != p) {
break;
}
update[i]->forward[i] = p->forward[i];
}
delete p;
while (level > 0 && head->forward[level] == tail) --level;
--length;
return true;
}
V &operator[](const K &key) {
V v = find(key);
if (v == tail->value) insert(key, 0);
return find(key);
}
V &find(const K &key) {
SkipListNode<K, V> *p = head;
for (int i = level; i >= 0; --i) {
while (p->forward[i]->key < key) {
p = p->forward[i];
}
}
p = p->forward[0];
if (p->key == key) return p->value;
return tail->value;
}
bool count(const K &key) { return find(key) != tail->value; }
};
int main() {
SkipList<int, int> L;
map<int, int> M;
clock_t s = clock();
for (int i = 0; i < 1e5; ++i) {
int key = rand(), value = rand();
L[key] = value;
M[key] = value;
}
for (int i = 0; i < 1e5; ++i) {
int key = rand();
if (i & 1) {
L.erase(key);
M.erase(key);
} else {
int r1 = L.count(key) ? L[key] : 0;
int r2 = M.count(key) ? M[key] : 0;
assert(r1 == r2);
}
}
clock_t e = clock();
cout << "Time elapsed: " << (double)(e - s) / CLOCKS_PER_SEC << endl;
// about 0.2s
return 0;
}
# 跳表的随机访问优化
访问跳表中第k个节点,相当于访问初始有序链表中的第k个节点,很明显这个操作的时间复杂度是O(n)的,并不足够优秀。
跳表的随机访问优化就是对每一个前向指针,再多维护这个前向指针的长度。假设 A和 B都是跳表中的节点,其中A为跳表的第a个节点,B为跳表的第b个节点 ,且在跳表的某一层中A的前向指针指向B,那么这个前向指针的长度为b-a。
现在访问跳表中的第k个节点,就可以从顶层开始,水平地遍历该层的链表,直到当前节点的位置加上当前节点在该层的前向指针长度大于等于k,然后移动至下一层。重复这个过程直至到达第一层且无法继续行操作。此时,当前节点就是跳表中第k个节点。
这样,就可以快速地访问到跳表的第k个元素。可以证明,这个操作的时间复杂度为O(logn)。
